AUC若干计算方法及Python实现
根据ROC曲线下的面积计算AUC
该方法的原理参考上一篇文章关于AUC的讲解。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35def auc(labels, preds):
def roc(labels, preds):
n_pos = sum(labels)
n_neg = len(labels) - n_pos
labels_preds = zip(labels, preds)
labels_preds = sorted(labels_preds, key=lambda x: x[1], reverse=True)
threshold_list = sorted(list(set([0, 1] + preds)), reverse=True)
fpr_list = []
tpr_list = []
for threshold in threshold_list:
confusion_matrix = [[0, 0], [n_pos, n_neg]]
for i in range(len(labels_preds)):
if labels_preds[i][1] >= threshold:
if labels_preds[i][0]:
confusion_matrix[0][0] += 1
confusion_matrix[1][0] -= 1
else:
confusion_matrix[0][1] += 1
confusion_matrix[1][1] -= 1
tpr_list.append(confusion_matrix[0][0] / (confusion_matrix[0][0] + confusion_matrix[1][0]))
fpr_list.append(confusion_matrix[0][1] / (confusion_matrix[0][1] + confusion_matrix[1][1]))
return fpr_list, tpr_list, threshold_list
fprs, tprs, threshold = roc(labels, preds)
fprs_tprs = sorted(zip(fpr, tpr), key=lambda x: x[0])
area = 0
for i in range(1, len(fpr_tpr )):
area += (fprs_tprs [i - 1][1] + fprs_tprs [i][1]) * (fprs_tprs [i][0] - fprs_tprs [i - 1][0]) / 2
return area
根据AUC的另一意义
AUC的另一意义:表示对于一个二分类模型,取任意一个正样本和负样本,正样本的模型输出(score)大于负样本的模型输出的概率。即可通过求出这个概率值来计算AUC。
设样本中有M个正样本,N个负样本,模型对样本的输出为score。存在(M*N)个正负样本对。对每一个正样本,统计负样本中样本的score比该正样本score小的负样本个数,最后除以总的正负样本对,得到所要求的概率值,即为AUC。
可以简介的表示为:
实现细节:按照score对样本排序,然后对每个正样本,统计该正样本score比小的负样本1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19def auc(labels, preds):
"""
先排序,然后统计有多少正负样本对满足:正样本预测值 > 负样本预测值,再除以总的正负样本对个数
复杂度 O(NlogN)
"""
n_pos = sum(labels)
n_neg = len(labels) - n_pos
labels_preds = zip(labels, preds)
labels_preds = sorted(labels_preds, key=lambda x: x[1])
accumulated_neg = 0
statisfied_pair = 0
for i in range(len(labels_preds)):
if labels_preds[i][0] == 1:
statisfied_pair += accumulated_neg
else:
accumulated_neg += 1
return statisfied_pair / (n_neg * n_pos)
基于rank计算AUC
该方法其实也是基于AUC的物理意义来计算。区别是先计算了每个正样本的rank值,然后根据rank值统计正样本score大于负样本score的样本对。
设样本中有M个正样本,N个负样本,模型对样本的输出为score。
对于正样本中score最高的,排序为$rank_1$,比该正样本score小的有$M-1$个正样本,$rank_1-M$个负样本。
同理,对于正样本中score第二高的,排序为$rank_2$,比该正样本score小的有$M-2$个正样本,$rank_2-(M-1)$个负样本,
以此类推,正样本中score最小的,排序为$rank_M$,比该正样本score小的有0个正样本,$rank_M-1$个负样本。
总共有$M*N$个正负样本对,则所有满足条件的正负样本对的个数为: $(rank_1-M + rank_2 - (M-1) + … + rank_M - 1)/(M*N)$
化简之后可以得到AUC的计算公式:
例子: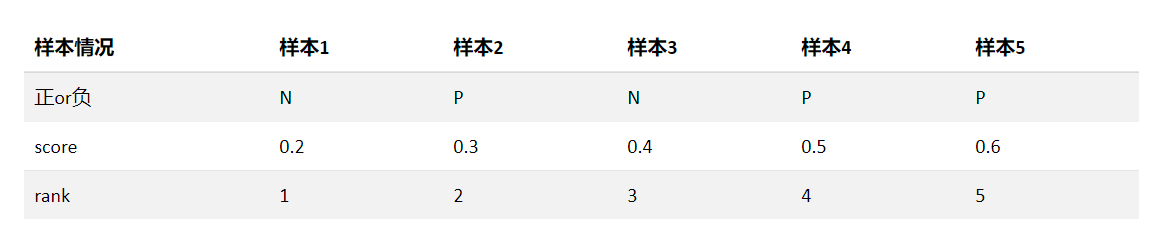
对该例:$AUC=\frac{(2+4+5) - (0.5\times 3\times 4)}{3 \times 2} = 0.833$1
2
3
4
5
6
7
8
9def auc(labels, preds):
n_pos = sum(labels)
n_neg = len(labels) - n_pos
labels_preds = zip(labels, preds)
labels_preds = sorted(labels_preds, key=lambda x: x[1])
rank = [label for (label, pred) in labels_preds]
rank_list = [i+1 for i in range(len(rank)) if rank[i] == 1]
auc = (sum(rank_list) - (n_pos * (n_pos + 1)) / 2) / (n_neg * n_pos)
return auc