排列组合问题

排列问题

排列： 一般地，从n个不同元素中取出m（m≤n）个元素，按照一定的顺序排成一列，叫做从n个元素中取出m个元素的一个排列(permutation)。特别地，当m=n时，这个排列被称作全排列(all permutation)。

数组的全排列

我们以[1,2,3]为例，首先我们从数组中选取数字1，然后和剩下的[2,3]组成的子排列构成全排列；然后从数组中选取数字2，然后和剩下的[1,3]组成的子排列构成全排列；最后从数组中选取数字3，然后和剩下的[1,2]组成的子排列构成全排列。详细的递归过程如下：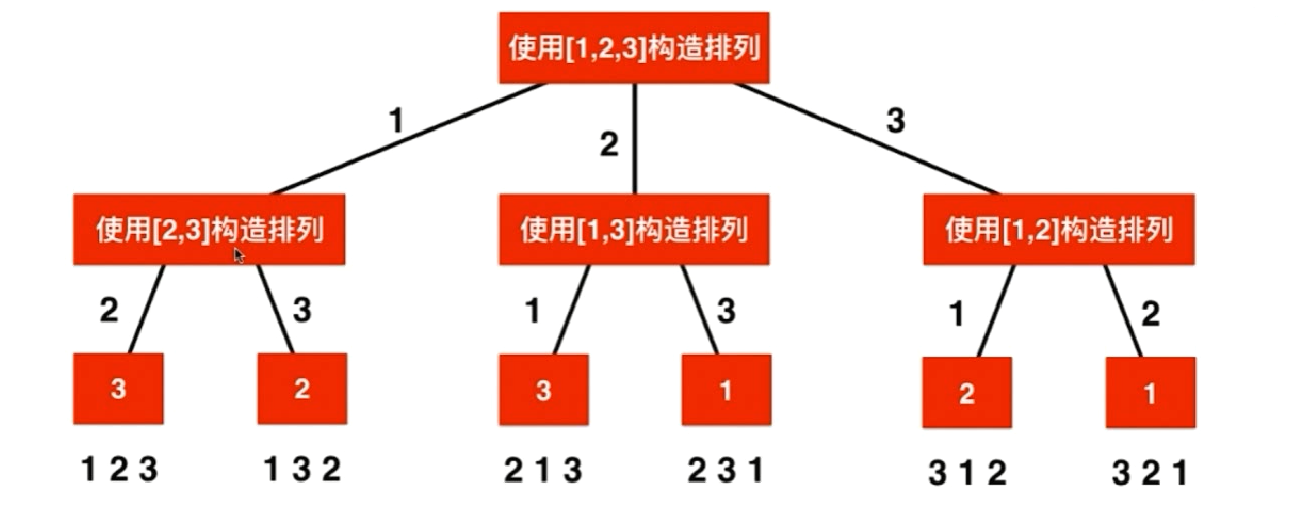

代码实现细节：
index表示向当前排列添加第index个元素。
p表示当前的排列，其中拥有index-1个元素。
当index与数组长度相等时，说明一个全排列构造完成，保存该排列。否则，从array数组中选出一个未出现在p中的元素，加入当前排列，然后函数继续添加下一个位置的元素。
注意： 使用当前元素构造排列完成保存后，要将该元素弹出。

def permute(array):
    res = []
    # p表示当前生成的排列
    def generatePermutation(array, index, p):
        if index == len(array):
            res.append(p.copy())
            return
        for i in array:
            if i not in p:
                p.append(i)
                generatePermutation(array, index+1, p)
                p.pop()
    generatePermutation(array, 0, [])
    return res

普通排列

从上文的全排列可以很容易的推广到普通的排列，只需要更改上面代码的排列构造完全的条件即可，
当index等于k时，当前的排列即构造完成，保存，实现代码如下：

def permute(array, k):
    res = []
    def generatePermutation(array, index, p):
        if index == k:
            res.append(p.copy())
            return
        for i in array:
            if i not in p:
                p.append(i)
                generatePermutation(array, index+1, p)
                p.pop()
    generatePermutation(array, 0, [])
    return res

重复排列

重复排列(permutationwith repetiton)是一种特殊的排列。从n个不同元素中可重复地选取m个元素。按照一定的顺序排成一列，称作从n个元素中取m个元素的可重复排列。当且仅当所取的元素相同，且元素的排列顺序也相同，则两个排列相同。只需将上面普通排列代码中判断数组元素是否在当前排列中的条件去掉即可，实现代码如下：

def permute(array, k):
    res = []
    def generatePermutation(array, index, p):
        if index == k:
            res.append(p.copy())
            return
        for i in array:
            p.append(i)
            generatePermutation(array, index+1, p)
            p.pop()
    generatePermutation(array, 0, [])
    return res

组合问题

组合： 一般地，从n个不同的元素中，任取m（m≤n）个元素为一组，叫作从n个不同元素中取出m个元素的一个组合。

数组的组合

我们以[1,2,3，4]中取2个数为例。在[1,2,3,4]中取1与排序相同，与排列不同的是，组合不考虑取出元素的顺序，所以在[1,2,3,4]中取2之后，只能在[3,4]中继续取值，因为之前已经计算出了所有包含1的组合。同理在[1,2,3,4]中取3之后，只能在[4]中取值。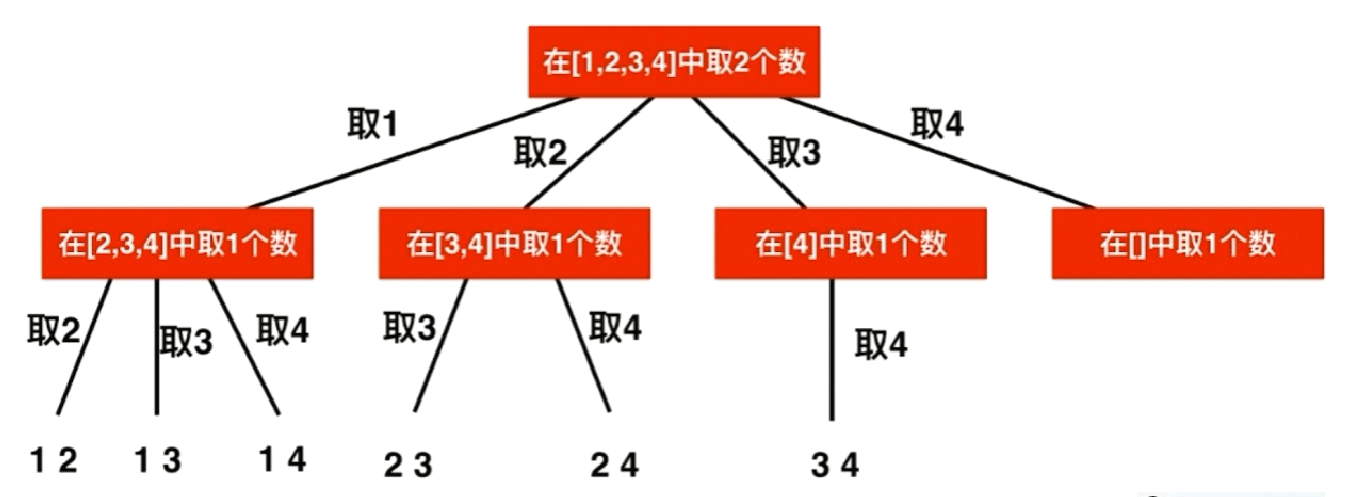

start表示需要从数组的start位置开始搜索元素加入当前组合c中。
c表示当前的组合。
当当前组合的长度等于k时，组合构造完成。

def combine(nums, k):
    res = []

    def generateCombinations(nums, start, c):
        if len(c) == k:
            res.append(c.copy())
            return
        for i in range(start, len(nums)):
            c.append(nums[i])
            generateCombinations(nums, i+1, c)
            c.pop()
        return
    generateCombinations(nums, 0, [])

    return res

应用

LeedCode-Combination Sum

给出一个集合，其中所有的元素各不相同，以及一个数字T。寻找所有该集合中元素组合，使得组合中所有的元素和为T（集合中每一个元素可以使用多次）

给定集合nums=[2,3,6,7], T=7`
返回[[7],[2,2,3]]

index表示从集合的index的位置往后查找候选元素

class Solution:
    def combinationSum(self, candidates, target):
        """
        :type candidates: List[int]
        :type target: int
        :rtype: List[List[int]]
        """
        res = []

        def fun(candidates, index, target, cur_res):
            if target == 0:
                res.append(cur_res.copy())
                return
            for i in range(index, len(candidates)):
                if target >= candidates[i]:
                    cur_res.append(candidates[i])
                    # 由于每个元素可以使用多次，所以下次寻找候选元素还是从当前位置继续，而不是从下一个位置继续
                    fun(candidates, i, target-candidates[i], cur_res)
                    cur_res.pop()

        fun(candidates, 0, target, [])
        return res

LeetCode-Subsets

给出一个集合，其中所有的元素各不相同。求出该集合的所有字集。

给定集合nums=[1,2,3]
返回[[], [1], [2], [3], [1,2], [1,3], [2,3], [1,2,3]]

第一种解法，n个元素的子集可以看做是$C_n^0, C_n^1,C_n^2,\cdots,C_n^k,\cdots,C_n^n$所有排列的集合，则在实现上与组合问题的区别即为不用判断当前当前的结果是否等于k，因为求子集需要k把0到n所有的数都要取一遍。

class Solution:
    def subsets(self, nums):
        """
        :type nums: List[int]
        :rtype: List[List[int]]
        """
        res = []
        
        def fun(nums, start, cur_res):
            res.append(cur_res.copy())
            for i in range(start, len(nums)):
                cur_res.append(nums[i])
                fun(nums, i + 1, cur_res)
                cur_res.pop()

        fun(nums, 0, [])
        return res

第二种解法，对每个元素，有两种可能，加入当前组合和不加入组合

class Solution:
    def subsets(self, nums):
        """
        :type nums: List[int]
        :rtype: List[List[int]]
        """
        res = []
        
        def fun(nums, index, cur_res):
            if index == len(nums):
                res.append(cur_res.copy())
                return
            # 将当前元素不加入该组合
            fun(nums, index+1, cur_res)
            # 将当前元素加入该组合，
            cur_res.append(nums[index])
            fun(nums, index+1, cur_res)
            cur_res.pop()

        fun(nums, 0, [])
        return res

算法之排列组合问题